最近在玩一个叫《哈利波特》的手游,这是一个卡牌游戏,游戏内有一个禁卡机制,每周会由部分满足一定条件的玩家以投票的方式决定下一周中哪些卡会被禁用。在我玩的过程中,发现每次投票结果出来之后,结果总是出乎意料,即普遍认为过于强势、不喜欢的卡牌票数并不高,反而一些常见而实用性强的卡牌被禁用了,在各大游戏论坛上每周都有人对投票的结果产生讨论,大家都对这样的投票结果甚至投票机制产生了怀疑。这件事让我想起了不久之前在机核网听过的一期关于投票机制的电台节目,有感于此,我又去听了一遍,有了更深的理解,这里总结整理一下。 (原电台链接点击这里,如果懒得听,可以直接看本文的总结)
最常见的投票方式——简单多数
我们常见的最普遍的一种投票方法就是“简单多数投票”。简而言之,就是给出很多选项,每个人在其中选择一项进行投票,最后得票数最高的一项胜出。这个投票方式是很常见的,像我前面提到那个游戏里的投票就是这样,还有常见小到群投票、微信公众号内的各种亲戚朋友的作品、节目之类的活动投票,大到美国总统选举。
这样的投票机制很大的优点就是简单。的确,方法很简单,也不用有过多的操作,只要列出选项,大家一顿投,然后找出票数最高的就可以了。但正是这么简单的机制,存在很多很多问题。
假设现在有100个选项,有1000个人来投,那么平均平均每个选项就是10票。现实情况虽然不一定这么极端平均,但是最终胜出结果的票数占比必然不会很高。假如最高票占15%,那么投其他选项的票数就占85%。虽然他的票数是所有选项里面最多的,但是并不足以服众。不管那15%的人有多喜欢他,总是有85%的人不喜欢他。不管怎样投票,不管结果是哪个胜出,最终结果必然是大部分人都不喜欢的结果。用一句话总结简单多数投票结果就是
众多一小撮中的最大那一撮
此外还有一个问题。假如现在投票前3名分别是ABC,有100个人来投票。因为种种原因,现在A的呼声最高,其次是B,再次是C。那么这100个人里面,喜欢C且讨厌A/B的人,就开始慌了——自己明明最喜欢C,但是C显然无法获胜了。C赢不了也就算了,现在A和B都有机会赢,那怎么办呢?这些人之中,更讨厌A,没那么讨厌B的人,会选择全票投给B;同样的,更讨厌B,但没那么讨厌A的人,又会把票投给A。明明这些人是喜欢C的,却昧着良心选择了A和B,这种情况就叫做“策略性投票”。即,投票人没有投自己真正想投的,而因为一些利益关系而变得不诚实了,大家无法表达自己真实的想法了。比较典型的的例子就是美国总统大选,希拉里和特朗普,虽然大家对特朗普了解不多,但真的很讨厌希拉里,所以最终结果搞出了这么一个奇葩总统。因此,简单多数投票会导致的“策略性投票”,用一句话总结就是
两害相权取其轻
乍一看好像有那么回事——复选排序法
既然简单多数投票法的结果必然是大部分人不喜欢的,那么有没有一种方法让最终的结果所得的票数超过50%,也就是大部分人都喜欢呢?这就是复选排序法。复选排序法是指,所有人投票时,不再是做选择了,而是列一个清单,把投票选项按自己的喜好做一个排序。在所有人投完票后,根据排序的结果,重复进行几轮计票,最终选出一个得票数过半的选项。
举个例子,假如现在有5个选项,100个人投票,每个人投票时,给五个选项按喜好程度排序,比如有的人投 A C D B E ,有的人投E B A C D,全部投完票之后,我们先以所有人的第一顺位,也即最喜欢的那一项来进行统计各个选项的得票数,结果如下:
| A | B | C | D | E |
|---|---|---|---|---|
| 30 | 25 | 20 | 15 | 10 |
现在的结果是,A最多,30票,但是未超过半数;E最少,只有10票。第一轮统计完后,E被淘汰,那么就来看看这10票的投票结果。因为这10个人的第一顺位投了E,而E被淘汰了,那么就把他们的第一顺位划掉,看第二顺位投了什么,依次分票给其余四个选项。假设这10个人的第二顺位,有6个人选了B,4个人选了D,那么分票后的结果是:
| A | B | C | D | E |
|---|---|---|---|---|
| 30 | 31 | 20 | 19 | x |
第二轮的结果,B变成了最多的31票但是仍未超过半数,那么就再把最后一名D淘汰掉,再来看选了D的这些人,他们的第二顺位填了什么。如果他们第二顺位选了已经被淘汰掉的E,那就接着看第三顺位。假如这19人,第二顺位(除去已经淘汰掉的E)全都选了B,那么分票后B就超过了50票,过半数,直接获胜;如果是其他情况,还没有一个选项超过半数,那就接着找一个票数最低的选项淘汰,以此类推,直到出现一个选项他的票数超过了一半。
漏洞百出的复选排序法
复选排序法乍一看好像有那么回事,很科学,但是实际上却还是存在着很多严重的缺点,从根本上无法满足很多投票中的原则。
单调性原则
单调性原则是指:
投票者不能为一个选项投票而反过来伤害这个选项。
这是一个很显而易见的原则,我投票肯定是为了他好,不能害了他,但是实际上用复选排序法却真的会有这种背道而驰的情况发生,举一个例子:
假如有三个选项,17个人,用复选排序法,现在的投票结果是这样:

1到17是这17个投票者的编号,按顺序从上到下是他们投票的顺位。可以看到,第一轮结束,第一顺位填A的有6个,B的有6个,C的有5个,C最少,那就把C淘汰掉,再把选了C的人的票进行分票,结果如下:

现在票数最高的是A,有11票,超过半数,直接取胜。
这是一个正常的情况,现在来考虑一些其他情况。假如时光倒流,重新投票,其他人不变,16号和17号两个人本来就在纠结选A还是选B,再三思考之下,还是觉得更喜欢A,想支持支持A,就把A填到了第一顺位上,而第二顺位填了B。现在的结果是这样:

可以看到,在16和17号第一顺位不填B而改填A之后,第一顺位得票最高的A最多,有8票,还是没有超过半数;而票数最少的却变成了B,只有4票,面临淘汰。而在B被淘汰并分票后的结果变成了这样:

诶???这个时候C变成了票数最高的,有9票,超过了半数,直接胜出!这下16号和17号可傻眼了,这俩人本来只是纠结于A和B谁更好,经过思考把A和B的顺序换了下,结果是他俩最不喜欢的C获胜了。
在这个例子中,C在第二次投票中获胜的原因就是他虽然在第一志愿中选的人不是最多的,但是他确保了分票的那些人的第二志愿选了他,最终导致了16 17两个人投票产生了相反的结果。
多数原则
多数原则是指:
最终获胜的选项,应对是超过50%的人支持的
再举一个简单的例子,假如现在有三个选项ABC,在经过复选排序投票之后发现,第一志愿选A的占比49%,第一志愿选B的占比49%,第一志愿选C的占比2%。在第二志愿中,选C的占比98%,选A和B的各占1%。这个结果显而易见,首轮淘汰的就是C了。但是无论最终的结果是A还是B,这里都有一个问题,虽然C在第一志愿中占比少的可怜,但是他在第二志愿中的占比接近了100%,也就是说几乎所有人都觉得C还不错,虽然在他们看来可能比A或者B差点,但是98%的占比已经足以说明C的支持率有多高了,然而就是这样一个“老好人”,第一轮就被淘汰了。
在这个例子中可以看到,虽然通过顺序可以表明自己选择的重要性程度,但是除了第一顺位之外的顺位貌似没有表现出什么分量,也即二三顺位的权重无效了。不管你在第二顺位中的支持率有多高,只要第一顺位低一些,直接就淘汰了。在这种情况下,假如我们只看第一顺位,A和B都无法获胜;假如第一轮过后C没有淘汰,在第二顺位支持C的人数可是多达98%,确实符合了多数原则,但是事实上,他在第一轮就被淘汰了。
那么这个问题这么解决呢?很简单,问题出在后面的顺位没有意义了,那么我们只需要赋予顺位更多的意义就可以了,也就是说,每一个顺位可以加对应的权重,比如第一顺位的给10分,第二顺位的给5分,第三顺位的给3分。再回到刚才那个场景,假如是100个人投票,那么第一顺位选A和B的各有49人,没人算10分,也就是总分490分;第二顺位选C的有98人,每人5分,总分也是490分。此外还有第一顺位选C和第二顺位选AB的,最终总分得出C为510分,A和B都是495分,这样一来获胜者就是C了。
给顺位加权重看似可以解决顺位权重无效的问题,那么问题来了,具体每个顺位的权重是多少,由谁来定呢?假如第一顺位100000分,第二顺位1分,那上面那个例子中C还不是一样被淘汰?第一顺位10分,第二顺位9分,那C不是获胜的更容易了些?是的,正是因为这个权重很难去定义,所以一旦采用了这种规则,那么投票就变成了看权重分数对于哪个顺位的人有利。这个用排序+权重来投票的机制,叫做 波达计数法。即使权重的分数定的再合理,此时最终获胜的选项显然不再是一定有50%以上人支持的了,而是权重分最高的了,因此也还是无法满足多数原则。
孔多塞原则
孔多塞原则是指:
一个选项如果能获胜,那把他拿出来挨个和其他选项做一对一的比较,应当也能获胜。或者说,一个选项单拿出来跟其他选项做一对一的比较如果都获胜了,那他应当是最终的获胜者
这是一个非常显而易见的原则,亦是一个悖论。还是举个例子,有3个选项,3个人来用复选排序法投票,现在结果如下:
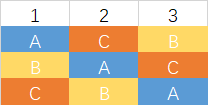
我们用孔多塞原则来看,首先只拿A和B做比较,1选择A>B,2选择A>B,3选择B>A,A获胜;再拿A和C对比,1选择A>C,2选择C>A,3选择C>A,C获胜;再来对比B和C,1选择B>C,2选择C>B,3选择B>C,B获胜。我们会发现,ABC好像都没法完胜每个其他选项,形成了一个循环。每个人都很清楚自己的选择,也不会形成死循环,但是当所有人的选择合在一起时,就出现了循环,无解,这就是孔多塞悖论。在这种情况下,假如我们采用“先拿两个选项1对1比较,胜出的选项再跟另外的选项挨个1对1比较”这种方式来选择我们最终的结果,那么比较的顺序就至关重要了。在上面这个例子中,如果选用A和B比较,最后再和C比较,结果就是C获胜了。但是假如先拿B和C比较,再和A比较,那么结果就是A获胜了,也就是说投票的结果完全由发起比较的这个顺序来决定了,这是显然不应该出现的。
其他
还有其他原则,同样都是一个投票机制“很显然应当”满足的原则:
- 参与度原则:投票机制应当每个人都进行投票,而不能鼓励人们通过弃权来让最终的结果符合自己的预期
- 无关选项原则:在已有的选项和投票结果不变的情况下,引入一个新的选项,那这个新的选项应当不影响原来结果中的顺序
- 一致性原则:如果所有人都认为A比B好,那么无论最终的结果是什么,都应当还是符合A比B好的
- 反相对称原则:如果把所有人的投票顺序颠倒过来,拿最终的结果也应当精准的颠倒过来
没有完美
虽然只是举个两个投票机制为例子,但是这两种最常见也感觉最科学的投票机制都充满了漏洞。实际上正是这样,这个世界上并不存在完美的投票机制,每一个精心设计的投票机制都无法满足“显而易见”的原则。是不是这些原则本身不对呢?不是的,这些原则之所以设计出来,其实就是为了检验一个投票机制是否健全。这里引用一张图简单总结下投票机制:

共通的问题
实际上,除了这些针对投票结果而设计出的各种原则之外,从投票者这一角度,投票机制还有两个根本性的问题,是所有投票机制都很难满足的。这两个问题一个是 策略性投票 问题,在前面提到过,另一个是 代表性 问题。
策略性投票
无论你是采用什么投票机制,你能保证所有参与投票的人都是真心实意选择自己的结果的吗?不能,因为每个人在投票时,自己的结果都会或多或少受到一些因素影响,可能是因为利益,可能是受到信息的欺骗,也可能是受到胁迫,总之我们不能保证所有的票都是100%表达出自己真实想法的,这既是策略性投票问题。最典型的就是前面提到过的,“两害相权取其轻”,很多人为了不想要那个最差的结果,宁愿捏着鼻子选一个没那么差的,选一个稍好一些的。
代表性问题
在一些极小的场景下还好,但是在更大范围的投票中,不可能让每个人,每个个体都进来掺一脚,总是需要有人来代替部分人来进行投票的。小到一个奥斯卡电影投票,大到总统选举,都是由一些群体来作为代表,代表更广大的人们来投票的,而这些代表们,真的能名副其实的代表这些广大的人民吗?也不尽然。代表人可能是自己的局限,也可能受到一些外界的操控,最终他们投出来的结果,不会总是满足所有人的预期的。
代表性问题的例子就更多了,比如美国总统大选,特朗普VS希拉里,最终的结果,因为选举人票更多,特朗普赢了。但是统计整个美国每个人的投票,希拉里却是占优的。还有比如奥斯卡,奥斯卡投票提名电影,也不是全世界所有人都投的,总是会有部分人被选出来来代表大多数人。那么他们真的能不能代表好,取决于他们这些人的身份。如果代表人中年轻人多?可能结果就是漫威系列,速激系列等爆米花电影;代表人中老年人多一些,可能当初的《爱尔兰人》就获胜了;假如代表人中女性占了绝大多数,假如代表人中少数族裔占了多数,假如代表人中文艺青年占了绝大多数……总而言之,这个代表人的选择是很难去衡量的。
总结
总而言之,投票其实是个很复杂的东西,因为没有一种投票机制,他的投票者本身有完美的代表性,也没有一种投票机制产生的结果完美符合所有的标准、原则。但是话又说回来了,每个投票机制,虽然他所满足的原则不同,但是又各自有不同的优缺点。比如简单多数投票机制的结果,虽然不是很能服众,但是满足了一部分人的绝对支持;复选排序法虽然也有各种各样的不完美,但是却是一种“和稀泥”式的结果,能让大部分人觉得还行。我们能做的,应当是在特定的场合,采用更合适的投票机制。